Joint Probabilistic Matching Using m-Best Solutions
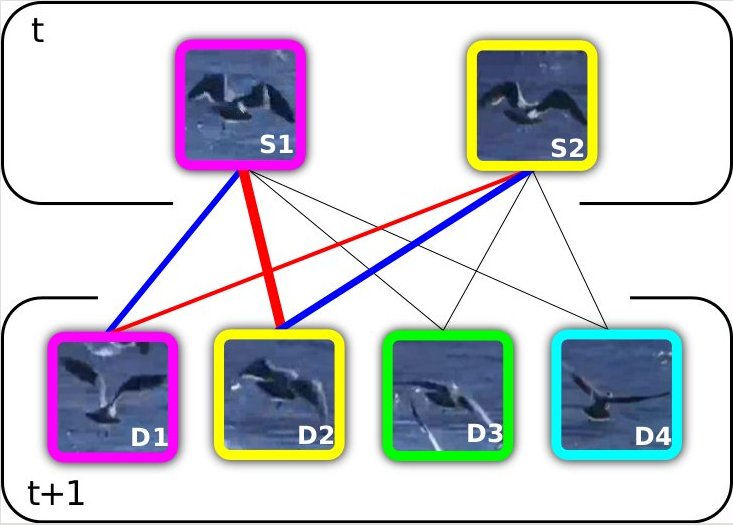
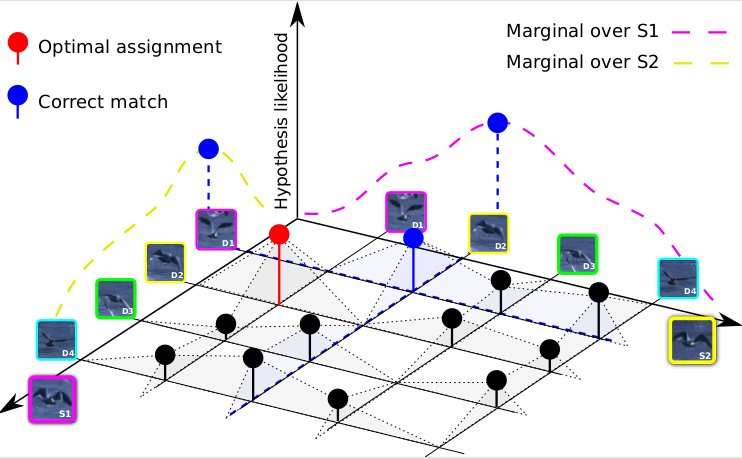
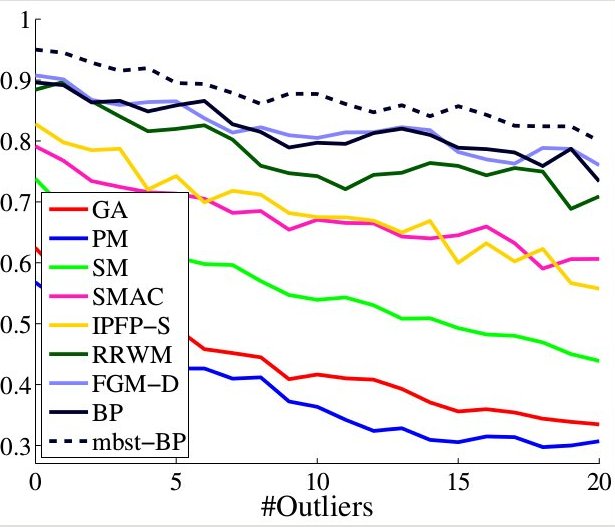
Abstract
Matching between two sets of objects is typically approached by finding the
object pairs that collectively maximize the joint matching score. In this paper,
we argue that this single solution does not necessarily lead to the optimal
matching accuracy and that general one-to-one assignment problems can be
improved by considering multiple hypotheses before computing the final
similarity measure. To that end, we propose to utilize the marginal
distributions for each entity. Previously, this idea has been neglected mainly
because exact marginalization is intractable due to a combinatorial number of
all possible matching permutations. Here, we propose a generic approach to
efficiently approximate the marginal distributions by exploiting the $m$-best
solutions of the original problem. This approach not only improves the matching
solution, but also provides more accurate ranking of the results, because of the
extra information included in the marginal distribution. We validate our claim
on two distinct objectives: (i) person re-identification and temporal matching
modeled as an integer linear program, and % (ii) multi-target
tracking-by-visual-matching, and (ii) feature point matching using a quadratic
cost function. Our experiments confirm that marginalization indeed leads to
superior performance compared to the single (nearly) optimal solution, yielding
state-of-the-art results in both applications on standard benchmarks.
References
Joint Probabilistic Matching Using m-Best Solutions
S. H. Rezatofighi,
A. Milan,
Z. Zhang,
A. Dick,
Q. Shi,
I. Reid
CVPR 2016 (oral presentation)
bibtex |
paper |
supplemental |
slides |
poster |
video
@inproceedings{Rezatofighi:2016:CVPR,
Author = {Rezatofighi, S. H. and Milan, A. and Zhang, Z. and Shi, Q. and Dick, A. and Reid, I.},
Booktitle = {CVPR},
Title = {Joint Probabilistic Matching Using m-Best Solutions},
Year = {2016}
}
Code
Joint Probabilistic Data Association Revisited

Abstract
In this paper, we revisit the joint probabilistic data association (JPDA)
technique and propose a novel solution based on recent developments in finding
the m-best solutions to an integer linear program. The key advantage of this
approach is that it makes JPDA computationally tractable in applications with
high target and/or clutter density, such as spot tracking in fluorescence
microscopy sequences and pedestrian tracking in surveillance footage. We also
show that our JPDA algorithm embedded in a simple tracking framework is
surprisingly competitive with state-of-the-art global tracking methods in these
two applications, while needing considerably less processing time.
References
Joint Probabilistic Data Association Revisited
S. H. Rezatofighi,
A. Milan,
Z. Zhang,
A. Dick,
Q. Shi,
I. Reid
ICCV 2015
bibtex |
paper |
code |
video 1
video 2
@inproceedings{Rezatofighi:2015:ICCV,
Author = {Rezatofighi, S. H. and Milan, A. and Zhang, Z. and Shi, Q. and Dick, A. and Reid, I.},
Booktitle = {ICCV},
Title = {Joint Probabilistic Data Association Revisited},
Year = {2015}
}